Doğrunun Analitik İncelenmesi
Analitik Geometri Hazırlık
Analitik Düzlem ve Dik Koordinat Sistemi
Dik kesişen iki sayı doğrusunun yerleştirildiği düzleme analitik düzlem denir.
Analitik düzlemde dik kesişen iki sayı doğrusunun oluşturduğu siteme dik koordinat sistemi denir.
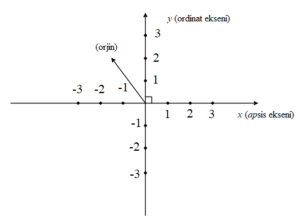
Koordinat sisteminde, yatay eksen olarak adlandırılan x ekseni apsis ekseni olarak bilinirken, dikey eksen olan y ekseni ordinat ekseni olarak adlandırılır.
Bu koordinat sisteminde, x (apsis) ve y (ordinat) eksenlerinin kesiştiği merkezi noktaya orijin veya başlangıç noktası denir.
Bir noktanın koordinatları P(a, b) ise, bu noktanın apsisi a ve ordinatı b’dir.
Ayrıca, x ekseni üzerindeki noktaların koordinatları (a, 0) şeklinde ifade edilir; y ekseni üzerindeki noktaların koordinatları ise (0, b) şeklindedir. Bu da demek oluyor ki, x ekseni üzerindeki bir noktanın ordinat değeri sıfırdır ve y ekseni üzerindeki bir noktanın apsisi sıfırdır.
Analitik Düzlemde Bölgeler
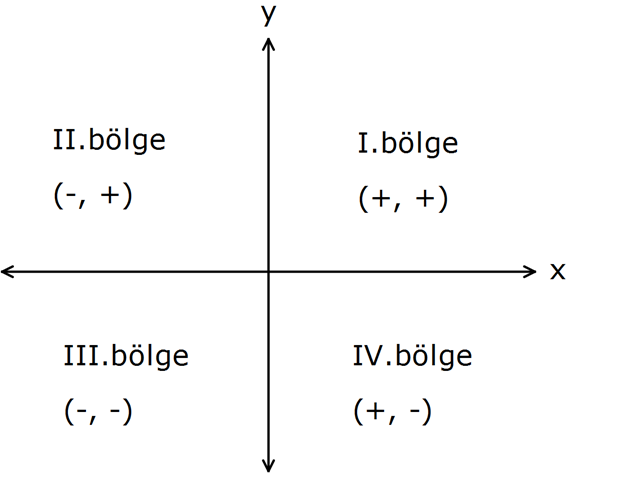
Koordinat sistemi, analitik düzlem üzerinde x ve y eksenlerinin dik olarak kesiştiği bir yapı oluşturur ve bu düzlemi 4 farklı bölgeye ayırır. Bu bölgeler, saat yönünün tersine doğru sırasıyla 1. bölge, 2. bölge, 3. bölge ve 4. bölge olarak adlandırılır.
Şekilde de görüldüğü gibi, A(x, y) koordinatlarına sahip bir nokta için:
- Eğer x ve y pozitifse, bu nokta 1. bölgededir.
- Eğer x negatif ve y pozitifse, bu nokta 2. bölgededir.
- Eğer x ve y her ikisi de negatifse, bu nokta 3. bölgededir.
- Eğer x pozitif ve y negatifse, bu nokta 4. bölgededir.
İki Nokta Arasındaki Uzaklık
Doğru Parçasını Belli Bir Oranda Bölen Noktanın Koordinatları
Bir Doğru Parçasının Orta Noktası
Bir Doğru Parçasını Belli Bir Oranda Bölen Noktanın Koordinatları
Analitik Düzlemde Doğrular
Doğrunun Eğimi ve Doğru Denklemleri
Bir Doğrunun Eğim Açısı ve Eğimi
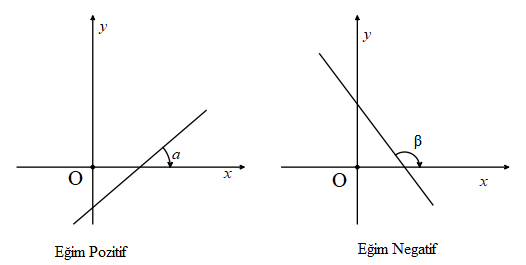
Bir doğrunun -x ekseni ile pozitif yönde (saat yönünün tersi) yaptığı açıya eğim açısı denir.
Eğim açısının tanjantı, o doğrunun eğimini verir.
tanα > 0 eğim sıfırdan büyük
tanβ > 0 eğim sıfırdan küçük
İki Noktası Bilinen Doğrunun Eğimi
Doğru Denklemleri
1. Eğimi ve Bir Noktası Bilinen Doğru Denklemi
2. İki Noktası Bilinen Doğrunun Denklemi
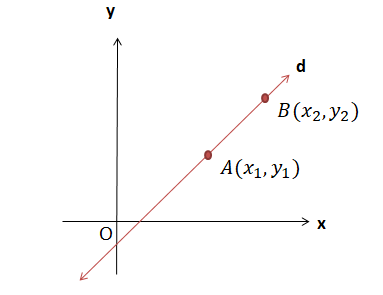
İki noktası bilinen doğrunun denklemini yazmak için;
İki noktadan geçen doğrunun eğimi bulunur.
Bulunan eğim ve verilen noktalardan herhangi biri kullanılarak doğru denklemi yazılır.
3. Eksenleri Kestiği Noktaları Bilinen Doğrunun Denklemi
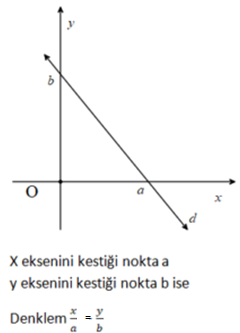
Doğru (a, 0) ve (0, b) noktalarından geçtiğine göre, doğrunun denklemi iki noktadan geçen doğru denklemi özelliği kullanılarak da yazılabilir.
4. Eksenlere Paralel Doğruların Denklemi
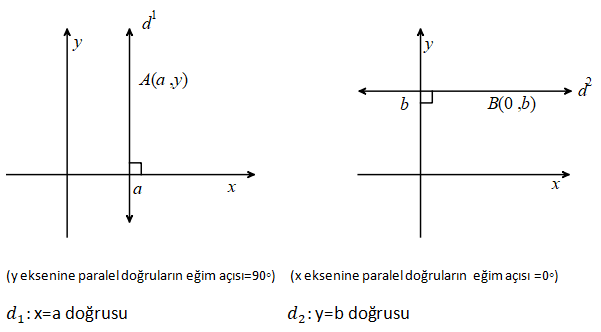
5. Orjinden Geçen Doğru Denklemi
Orijinden yani O(0,0) noktasından geçen doğrularda x = 0 için y = 0 olacağından
y = mx + n denklemindeki n terimi sıfır olur.
O halde orijinden geçen doğrunun eğimi m ise denklemi
y=mx
Doğru denklemi ax + by = 0 olur. Doğru denklemi ax + by + c = 0 şeklinde ise ve orijinden geçiyorsa c = 0 dır.
Doğru denklemi ax + by = 0 olur.
Denklemi Verilen Doğrunun Grafiği
Bir Noktanın Bir Doğruya Uzaklığı ve Paralel İki Doğru Arasındaki Uzaklık
Paralel Doğrular
Dik Doğrular
Kesişen Doğrular
