Üçgenler
Sınıf Matematik Üçgenlerde Kenarlar ve Açılar Konu Anlatımı
Üçgende Kenarlar ve Açılar
Üçgen ve Özellikleri
Günlük yaşamımızda birçok farklı yerde üçgen şekilleri bulabiliriz. Bir dağın silueti, bir çadırın tentesi, bir yoldaki trafik işareti veya bir kitabın köşesi gibi birçok nesne ve konsept üçgen biçiminde tasvir edilebilir.
Matematikte, üçgenler en sık karşılaştığımız geometrik şekillerden biridir. Diğer çokgenlerle ilgili özellikleri ortaya koymada yardımcı olan üçgenler, çokgenler arasında en az kenara sahip olanları temsil eder.
Örnek 2 :
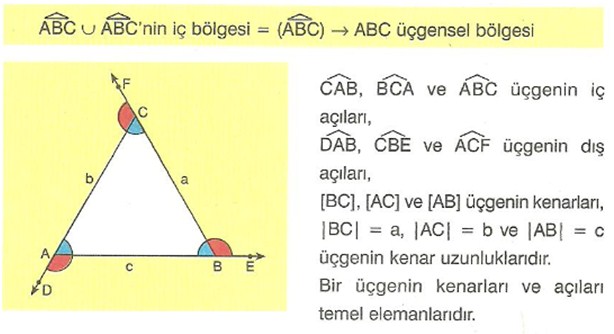
Üçgende Açılar
Örnek 2 :
Bir ABC üçgeninin dış açılarının ölçüleri toplamı 360° dir.
180° – x + 180° – y + 180° – z
= 540° – (x+y+z)
= 540° – 180° = 360°
Örnek 2 :
Bir ABC üçgeninin bir dış açısının ölçüsü, kendisine komşu olmayan iki iç açısın ölçüleri toplamına eşittir.
[AD // [BC], [BE // [CA], [CF // [AB]’dır.
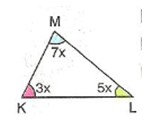
Örnek 1 : Bir KLM üçgeninin iç açılarının ölçüleri sırasıyla 3, 5 ve 7 ile orantılıdır. Buna göre en küçük açının ölçüsü kaç derecedir?
Örnek 2 :
Çözümü :
Açılar 3x, 5x, 7x olarak yazılırsa
3x + 5x + 7x = 180°
15x = 180°
X = 12° bulunur.
En küçük açı
3x = 3 . 12° = 36° dir.
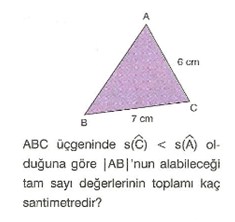
Sınıf Matematik Üçgenlerde Kenar Açı İlişkileri Konu AnlatımıÜçgenlerde Kenar Açı İlişkileriÜçgenlerde Kenar-Açı İlişkileri Örnek 2 :
ABC üçgeninde |BC|’nun alabileceği kaç tam sayı değeri vardır? Örnek 2 : 7 – 6 < |AB| < 7 + 6 |